知识点散记

若{z_0}\in{D}上,\lim_{z\rightarrow{z_0}}{\frac{f(z)-f(z_0)}{z-z_0}}存在，则可导
运算

([[2021秋季复变函数与积分变换期末试题答案.pdf#page=3&selection=244,1,250,0&color=yellow|2021秋季复变函数与积分变换期末试题答案, p.3]])
arg0 是没有定义的

复数的对数，指数运算，幂运算
- 对数
  
  Ln(z)=ln|z|+iArgz,与Ln(z)=lnz+2k\pi{i}
  - lnz=ln|z|+iargz
  - (cos\theta+isin\theta)^n=cos(n\theta)+isin(n\theta)
- 指数
  
  e^{z+2k\pi{i}}=e^z
- 幂
  
  z^a=e^{aLnz}=e^{alnz+a2k\pi{i}}=e^{alnz}e^{i2ak\pi}
C-R条件
- 对于z=u(x,y)+iv(x,y)
  \frac{\partial{u}}{\partial{x}}=\frac{\partial{v}}{\partial{y}}, \frac{\partial{u}}{\partial{y}}=-\frac{\partial{v}}{\partial{x}}
- 可进一步推出拉普拉斯方程（注意u,v的位置，方程中只有u或v）
  \frac{\partial^2u}{\partial{x^2}}+\frac{\partial^2u}{\partial{y^2}}=0,\frac{\partial^2v}{\partial{x^2}}+\frac{\partial^2v}{\partial{y^2}}=0
([[2020秋季复变函数与积分变换期末试题答案.pdf#page=2&selection=251,0,266,0&color=yellow|2020秋季复变函数与积分变换期末试题答案, p.2]])

若函数f(z)的实、虚部均为调和函数，则f(z)解析
错，是共轭调和。

([[2021秋季复变函数与积分变换期末试题答案.pdf#page=3&selection=390,0,420,1&color=yellow|2021秋季复变函数与积分变换期末试题答案, p.3]])

若函数f(z) 的实部与虚部满足C-R条件，则f(z)存在。
这是错的，还需要可微。

\delta(t)函数的性质
- \int^{+\infty}_{-\infty}f(t-t_0)\delta{(t)}dt=f(t_0)
- \delta(at)=\frac{1}{|a|}\delta(t)
- \int^{+\infty}_{-\infty}f(t)\delta^{(n)}{(t-t_0)}dt=(-1)^{n}f^{n}(t_0)
- \delta^{(n)}{(-t)}=(-1)^{n}\delta^{(n)}(t)
([[2021秋季复变函数与积分变换期末试题答案.pdf#page=2&selection=212,0,246,1&color=yellow|2021秋季复变函数与积分变换期末试题答案, p.2]])
广义傅里叶变换
- F(w)=F[f(t)]=\int^{+\infty}_{-\infty}f(t)e^{- iwt}dt
- F[\delta(t)]=1
- F(e^{iw_0t})=2\pi\delta{(w-w_0)}
- F(\delta{(t-t_0)})=e^{iwt_0}
幂级数\Sigma^{\infty}_{n=0}{a_n}z^n在z_0处收敛, 则在|z|<|z_0|内收敛，若在z_0处发散, 则在|z|>|z_0|外发散。
([[2020秋季复变函数与积分变换期末试题答案.pdf#page=1&selection=187,0,224,5&color=yellow|2020秋季复变函数与积分变换期末试题答案, p.1]])
留数
- 推广留数基本定理
  - 留数基本定理
    
    \sum\limits{Res[f(z),z_k]=\frac{1}{2\pi{i}}\oint_Cf(z)dz},孤立奇点z_k不包括无穷远点
    
    又因为
    
    Res[f(z),\infty]=-\frac{1}{2\pi{i}}\oint_Cf(z)dz
    
    得到
  - 若函数在扩充复平面内只有有限个孤立奇点，那么f(z)在各个孤立奇点（包括\infty点）的留数之和为0
    
    \sum^n_{k=1}{Res[f(z),z_k]}=0,孤立奇点z_k包括无穷远点
- 无穷远点留数的一些特殊性质(\infty是f(z)的孤立奇点)
  - Res[f(z),\infty]=-Res[f(\frac{1}{z})\frac{1}{z^2},0]
  - 对于一般f(z)的洛朗展开
    
    f(z)=\sum_{n=-\infty}^{+\infty}a_n(z-z_0)^n ,a_{n}=\frac{1}{2\pi{i}}\oint_C\frac{f(z)}{(z-z_0)^{n+1}}dz
    
    Res[f(z),z_0]=a_{-1}=\frac{1}{2\pi{i}}\oint_{C}f(z)dz
  - 而Res[f(z),\infty]=-a_{-1}
- 留数与极点
  - 对于m阶极点
    Res[f(z),z_{0}]=a_{-1}=\frac{1}{2\pi{i}}\oint_{C}f(z)dz=\frac{1}{(m-1)!}{\lim_{z \to z_0}{\frac{d^{m-1}}{dz^{m-1}}\{(z-z_0)^mf(z)}\}}
([[2019秋季复变函数与积分变换期末试题答案.pdf#page=3&selection=258,2,263,0&color=yellow|2019秋季复变函数与积分变换期末试题答案, p.3]]
计算题
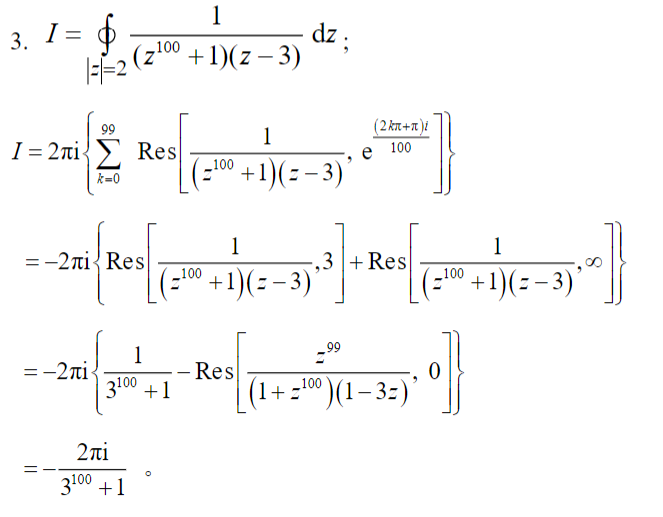
- 留数求解定积分
  - 三角
    - 三角替换
    - cos{\theta}=\frac{1}{2}({z+\frac{1}{z}})
    - sin{\theta}=\frac{1}{2i}({z-\frac{1}{z}})
    - d\theta=\frac{1}{zi}dz
  - 有理函数
    - 类下
  - e^{iax}
    - Im(z_k)>0,x_k为实数
    - \int^{+\infty}_{-\infty}R(x)e^{iax}dx=2\pi{i}\sum{Res[R(z)e^{iaz},z_k]}+\pi{i}\sum\limits{Res[R(z)e^{iaz},x_k]}
拉普拉斯变换求解微分方程
- 主要变换
  L[f^n(t)]=s^nF(s)-s^{n-1}f(0^+)-...-f^{(n-1)}(0^+)
- 常见变换
  - L(1)=\frac{1}{s}
  - L(e^{kt})=\frac{1}{s-k}
  - L(sinwt)=\frac{w}{s^2+w^2}
  - L(coswt)=\frac{s}{s^2+w^2}
  - L(t^{\alpha})=\frac{\Gamma(\alpha+1)}{s^{\alpha+1}}
- 逆变换
  - L^{-1}[F(s)]=\sum\limits{Res{[F(s)e^{st},s_k]}}
([[2021秋季复变函数与积分变换期末试题答案.pdf#page=6&selection=250,0,250,16&color=yellow|2021秋季复变函数与积分变换期末试题答案, p.6]])